How do you apply time-to-event analysis to compare the impact of different prescriptions on death?
- This article examines the survival function of two prescriptions using Kaplan-Meier and Cox models in an electronic health records (EHR) setting.
EHR data are powerful real-world data. They are conducive to time-to-event analysis owing to the characteristic of sequential visits to primary and secondary care services. Take UK’s OpenSAFELY for instance, this secure, transparent, and open-source platform provides an Trusted Research Environment (TRE) for National Health Service (NHS) EHR data analysis, which supported urgent research into the COVID-19 emergency.
Setting the Scene
Building on a hypothetical EHR data, this project aims to understand the impact of a prescription of proton pump inhibitor (PPI) versus a prescription for a histamine H2-receptor antagonist (H2RA) on all-cause mortality. To extract analysis data from various datasets of EHR and code lists, I use the following eligible criteria to define the study cohort:
- PPI and H2RA prescription with first prescription timeframe from 17 April 1997 to 17 April 2017
- the first prescription is after patient’s registration at general practice (GP) plus one year
- the first prescription is after the patient’s 18th birthday.
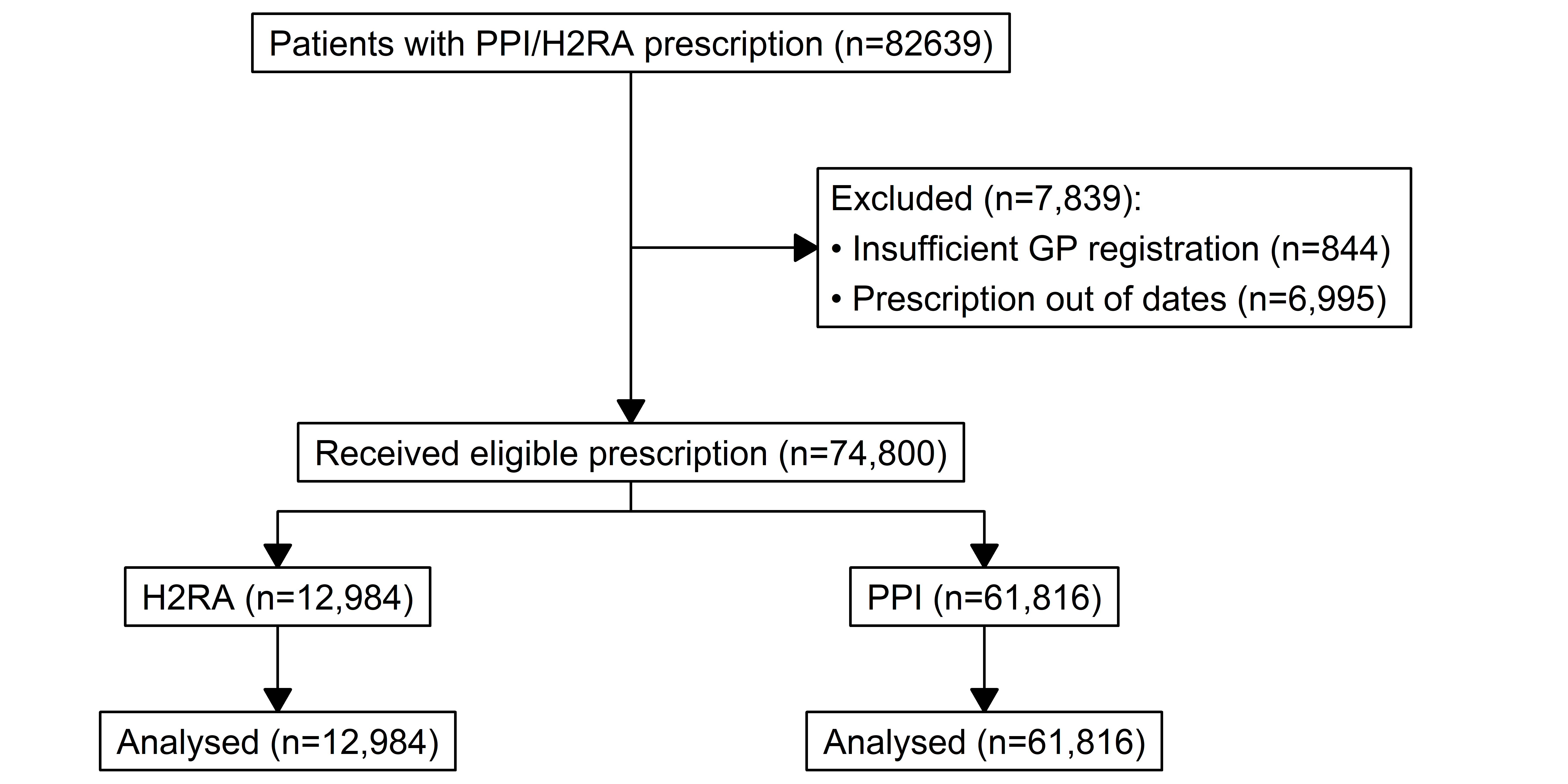
The study follow-up begins at the first prescription for PPI or H2RA, and it ends at the first of:
- death (event of interest)
- transfer out of GP
- end of study (17 April 2017), i.e. administrative censoring
Considering confounding effects, 10 potential confounding variables from the cohort are also examined: (1) age at prescription, (2) gender, (3) ethnicity, (4) Index of Multiple Deprivation (IMD), (5) body max index (BMI), (6) calendar year of first description, (7) diagnosis of gastric cancer prior to prescription, (8) gastro-oesophageal reflux disease (GERD) in the 6 months prior to prescription, (9) peptic ulcer in the 6 months prior to prescription, and (10) number of consultations in the year prior to prescription.
Notably, addressing missing data is an essential part of EHR data analysis. I adopt a strategy where patients’ birth dates are assumed to be on the 15th of June in the given birth year. Additionally, for BMI, I prioritize my-self-calculated BMI over those reported by GPs, while ensuring that the derived BMI values fall within an acceptable and realistic range of heights and weights.
Time-to-event Data
For the purpose of survival analysis, I define the length between index date (at first description) and end date (either death, censoring due to out of GP, or censoring due to end of study) as the days in the study.
From the perspective of exposure, the median length of follow-up is 4 years in PPI group and 9 years in H2RA group, respectively. The distribution of the length of follow-up is strongly right-skewed in the PPI group, whereas such distribution is not observed in the H2RA group.
Length of Follow-up by Prescription/Death in Years
| Subgroup | N | Median | IQR |
|---|---|---|---|
| PPI | 12,984 | 9 | 4.5-13.4 |
| H2RA | 61,816 | 4 | 0.5-6.1 |
| Death | 13,741 | 3.4 | 0.3-5 |
| Alive | 61,059 | 5.2 | 0.8-8.6 |
Disaggregated by outcome, those who are alive in the cohort period have longer follow-up (median 5.2 years), in comparison of the median 3.4 years for those who died.
Kaplan-Meier Method
To investigate the crude survival probability across two exposure groups, the non-parametric estimate of Kaplan-Meier is used. The probability of surviving 5 years or more is 0.888 (95% confidence interval, CI: 0.883-0.894) in H2RA group, whereas the probability of surviving 5 years or more is 0.796 (95% CI: 0.792-0.8) in PPI group.
The survivor functions in H2RA group are always higher than those in PPI group. As time goes by, the difference in survivor functions between the two groups increases, from 0.057 at year 1, to 0.109 at year 10, to 0.132 at year 19.
By using log-rank test, an overall lower survival probability in PPI group is confirmed (the chi-square statistic is 556 on 1 degree of freedom, p-value < 0.05), in comparison to H2RA group.
Cox Regression
Univariable Model
By fitting a univariable Cox proportional hazard model, a semi-parametric method, the log hazard ratio estimate is 0.52. The estimated hazard ratio is 1.68, which means the hazard for all cause death is increased by 68% in the PPI group relative to the H2RA group. The 95% CI (1.61-1.76), not covering null, indicates a strong evidence against the null hypothesis of no association between exposure and the hazard for death.
Note that the Cox Proportional Hazard (PH) assumption implies the hazard ratio measuring the effect of any predictor, i.e. prescriptions in this case, is constant over time.
Multivariable Model
Considering potential confounding, I examine whether the effect estimate, e.g. odds ratios in logistic regression, changes substantially after adding each candidate confounding variable in the Cox model. Also, for the purpose of survival curve estimation, certain non-confounding varaibles are selected into the multivariable Cox proportional hazard model.
Furthermore, to investigate whether the functional form for the continuous variable age is appropriate in the multivariable model, I calculate the Martingale residuals for age and number of consultations. However, it can be observed from the LOESS lines that direct employing a linear term for these continous varaible is appropriate.
In the final multivariable Cox PH model adjusting seven selected confounding ( below), the log hazard ratio estimate is 0.093. The estimated hazard ratio is 1.098 (95% CI: 1.049-1.150), meaning the hazard for all cause death is increased by 9.8% in the PPI group compared to the H2RA group. Compared to the univariable model, the effect of PPI is reduced in the multivariable model, yet still significant.
h(t│X) = h0 (t)exp{ β1*X{PPI}+β2*X{calendar period}+β3*X_{IMD person}+β4*X{gender} +β5*X_{ethnicity}+β6*X{recent GERD}+β7*X{number of consultations}+β8*X{age}
Xi:exposure for individual i (i=1,…,n); ti:death or censoring time for individual i; δ:indicator of death (1)or censoring (0).
Assessing the PH Assumption
I use the scaled Schoenfeld residual to assess the assumption of the multivariable Cox PH model. The null hypothesis in this test is that the corresponding β(t) coefficient does not vary over time, indicating that the proportional hazards assumption holds for that variable.
It can be observed that the hazard ratio is changing over time in some variables. The global Chi-square statistic in the Schoenfeld residual is 211 (p-value < 0.05), indicating this model in general didn’t follow the proportional hazard assumptions. For instance, in the beginning of follow-up, PPI’s hazard is similar to H2RA’s hazard, but the log hazard ratio of PPI is lower at later times.
Extended Cox Model
Since the assumption of the Cox PH model is violated, I use extended Cox model to accommodate the non-proportionality. This approach allows the hazard ratios to be dependent on time, i.e. interacting with time. After splitting cohort data into five-year chunks according to the adjusted years of follow-up in the study, we can see the hazard ratios of PPI over H2RA in 4 periods.
In the extended model, the overall hazard ratio is 1.165 in PPI group relative to H2RA group. However, using PPI-period 1 (year 0-5) as reference in the extended Cox model, the estimate of hazard ratio is 0.946 in the PPI-period 2 (year 5-10) group compared to H2RA group during the same period, with other covariate holding constant.
Estimating Survival Curve
To apply the extended Cox model to hypothetical patient profiles, imagine four scenarios:
- A man aged 50 in the white ethnicity group, with no co-morbidities and in the most deprived group.
- A man aged 50 in the white ethnicity group, with recent diagnosis of Gastroesophageal reflux disease (GERD) prior to prescription and in the least deprived group.
- As in 1. but for a woman.
- As in 2. but for a woman.
I plot the Cox survival curves in four scenarios by four periods, given this extended model is built upon time-dependent effect for the exposure. It can be observed that males (solid line) have lower survival functions compared to females (dashed line). In each scenarios during period 1, 2, and 3, the survival functions is lower in PPI group compared to H2RA group. However, in the period 4 (year 15 to 20), H2RA seems to have a higher risk of death, where its survival curve is under the PPI group.
Conclusion
EHR data are often used for survival analysis, either in parametic (Weibull), non-parametric (Kaplan-Meier), or semi-parametric (Cox) model. This article examines the observations which are times at which death occurs, in comparison of two prescriptions. Based on the extended Cox regression, hazard ratio gets increased by 16.5% in PPI group relative to H2RA group, whereas the hazard ratio is changing over time.
This article has been adapted from the assessment of the Analysis of Electronic Health Record module at LSHTM.
